Linear Regression With One Variable

         Linear Regression is one of the oldest and simplest Machine learning algorithms.  It is probably the first   Machine learning algorithm everyone learns in their Machine learning journey. It is used for predicting continuous values using previous data. Example- house price prediction, weather forecast, stock price prediction and many other kinds of predictions. Linear Regression is the core idea for many Machine learning algorithms. In this article, we will learn Linear Regression with one variable and how to optimize the algorithms for better predictions. So, without wasting any time let’s begin the article.

          Linear Regression is a supervised learning algorithm that is used for regression problems. It determines the       relationship between the dependent and the interdependent variables with the help of a best-fitting line; y = mx + c. It predicts a real number for given input variables.

It uses the following equation:

Here, X1, X2,..., Xn are the independent variables and yo is the dependent variable.

w1, w2,..., wn is the assigned weights, b is the bias and e is the error.

Take a look at the picture below.

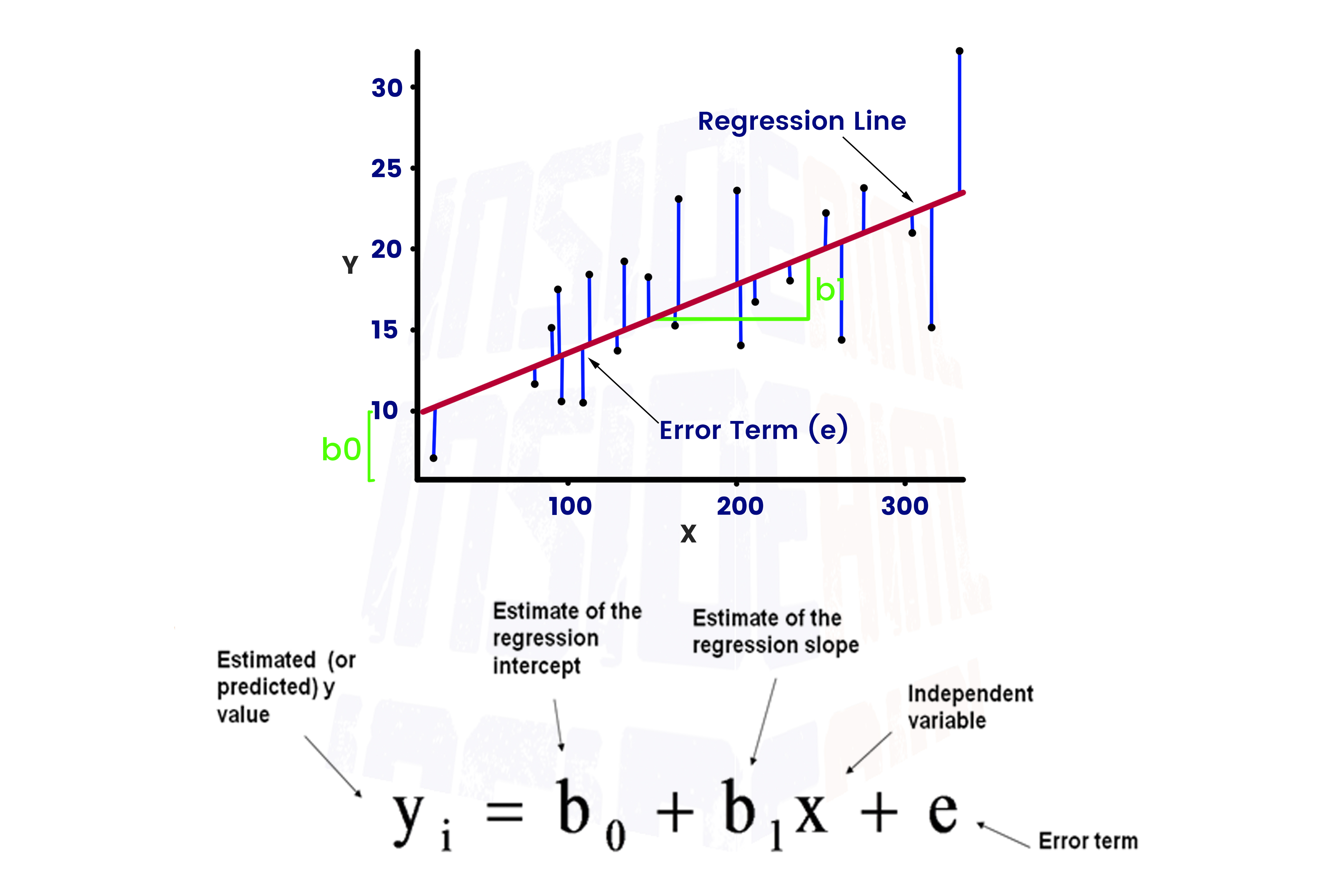
Here, b = bo, w1 = b1, and yo = yi 

Now, we have a basic idea of the Linear Regression equation. Let’s move on to Linear Regression with one variable.

        In the eqn1, we have n number of variables i.e X1, X2,..., Xn. Here, we will focus on Linear Equation with only one variable i.e X1.

        For example: let’s assume we have to predict the price of a used mobile phone and it completely depends upon its condition, the condition is a score from 1 to 5. Here, price is the dependent variable and condition is the independent variable.

The Linear Regression equation for the above case would be:

But in the real world, we don’t have just one variable, we have a number of variables for predicting the output with different weights(Wn). 

          Cost functions determine how good our model is at making predictions for a given set of parameters(w&b). To   train w and b we use the cost function. The values of w and b should be good enough such that the predicted value yo should be close to actual value y at least on training data.

Cost Function for Linear Regression with one variable.

Here, L(y0,y) is the loss function which is equal to-

Here, yo is the predicted value and y is the actual value. The value of the cost function should be as less as possible, fewer values means high accuracy.

          Gradient descent helps to learn w and b in such a manner that cost function is minimized. The cost function is of   convex nature means there is only one global minimum. Gradient descent tries to find out the global minima by updating the values of w and b in every iteration till global minima are achieved.

Take a look at the picture below.

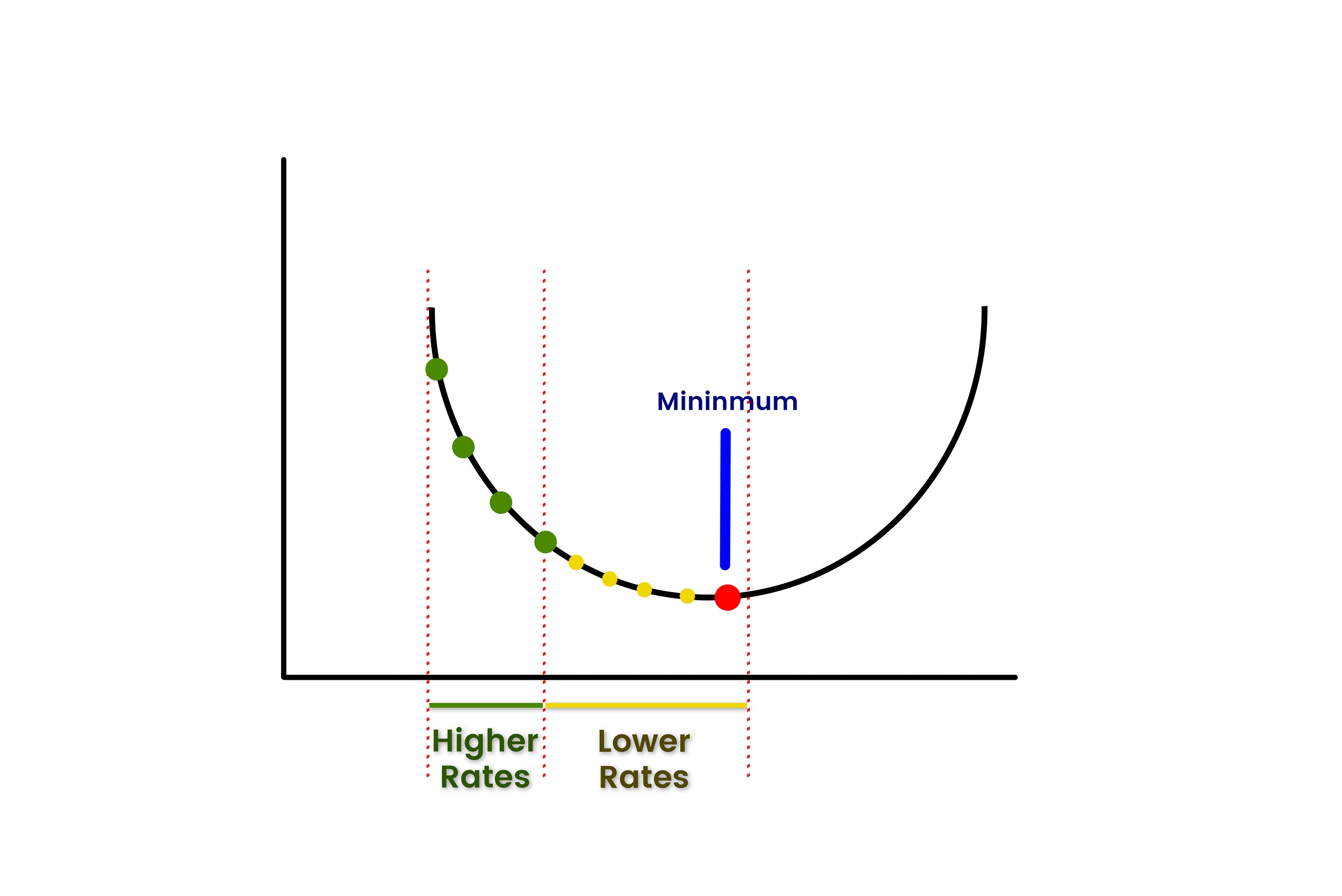
          In the above image for the initial values of w and b, we are at the first cross that is far away from the global minima/least possible value of cost function. Now, gradient descent will keep updating the values of w and b such that the cross started moving downhill. When we reach the global minima, the values of w and b will be the final values of parameters used for training the linear regression model. This is how Gradient descent works.

          In this article, we learned Linear regression, LR with one variable, cost function and gradient descent. In the  real world, we usually don’t have only one variable for predicting the output. We considered the case on the only variable here only to make you understand Linear regression easily. We discovered how we can find optimal values of parameters w and b using cost function and gradient descent. 

We hope you gain an understanding of what you were looking for. Do reach out to us for queries on our, AI dedicated discussion forum and get your query resolved within 30 minutes.

      

Liked what you read? Then don’t break the spree. Visit our insideAIML blog page  to read more awesome    articles. 

If you are into videos, then we have an amazing YouTube channel as well. Visit our InsideAIML Youtube Page to learn all about Artificial Intelligence, Deep Learning, Data Science and Machine Learning. 

Keep Learning. Keep Growing.